Last updated: 2018-05-17

Code version: 9333172

Loading required package: ashr
corrplot 0.84 loaded

The data contains 10 conditions with 10% non-null samples. For the non-null samples, it has equal effects in the first c conditions.

Let L be the contrast matrix that subtract mean from each sample.

\[\hat{\delta}_{j}|\delta_{j} \sim N(\delta_{j}, \frac{1}{2}LL')\] 90% of the true deviations are 0. 10% of the deviation \(\delta_{j}\) has correlation that the first c conditions are negatively correlated with the rest conditions.

We set \(c = 2\).

set.seed(1)
R = 10
C = 2
data = sim.mean.sig(nsamp=10000, ncond=C)

Ash 1 by 1

L = matrix(-1/R, R, R)
diag(L) = (R-1)/R
row.names(L) = colnames(data$Chat)
mash_data = mash_set_data(Bhat=data$Chat, Shat=data$Shat)
mash_data_L = mash_set_data_contrast(mash_data, L)
m.1by1 = mash_1by1(mash_data_L)

Discard last column

Mash contrast model

L.10 = L[1:(R-1),]
mash_data_L.10 = mash_set_data_contrast(mash_data, L.10)
U.c = cov_canonical(mash_data_L.10)

# data driven
# select max
m.1by1.10 = mash_1by1(mash_data_L.10)
strong = get_significant_results(m.1by1.10,0.05)
# center Z
mash_data_L.center = mash_data_L.10
mash_data_L.center$Bhat = mash_data_L.10$Bhat/mash_data_L.10$Shat # obtain z
mash_data_L.center$Shat = matrix(1, nrow(mash_data_L.10$Bhat),ncol(mash_data_L.10$Bhat))
mash_data_L.center$Bhat = apply(mash_data_L.center$Bhat, 2, function(x) x - mean(x))
U.pca = cov_pca(mash_data_L.center,2,strong)
U.ed = cov_ed(mash_data_L.center, U.pca, strong)

mashcontrast.model.10 = mash(mash_data_L.10, c(U.c, U.ed), algorithm.version = 'R', verbose = FALSE)

Using mashcommonbaseline, there are 288 discoveries. The covariance structure found here is:

barplot(get_estimated_pi(mashcontrast.model.10),las = 2, cex.names = 0.7)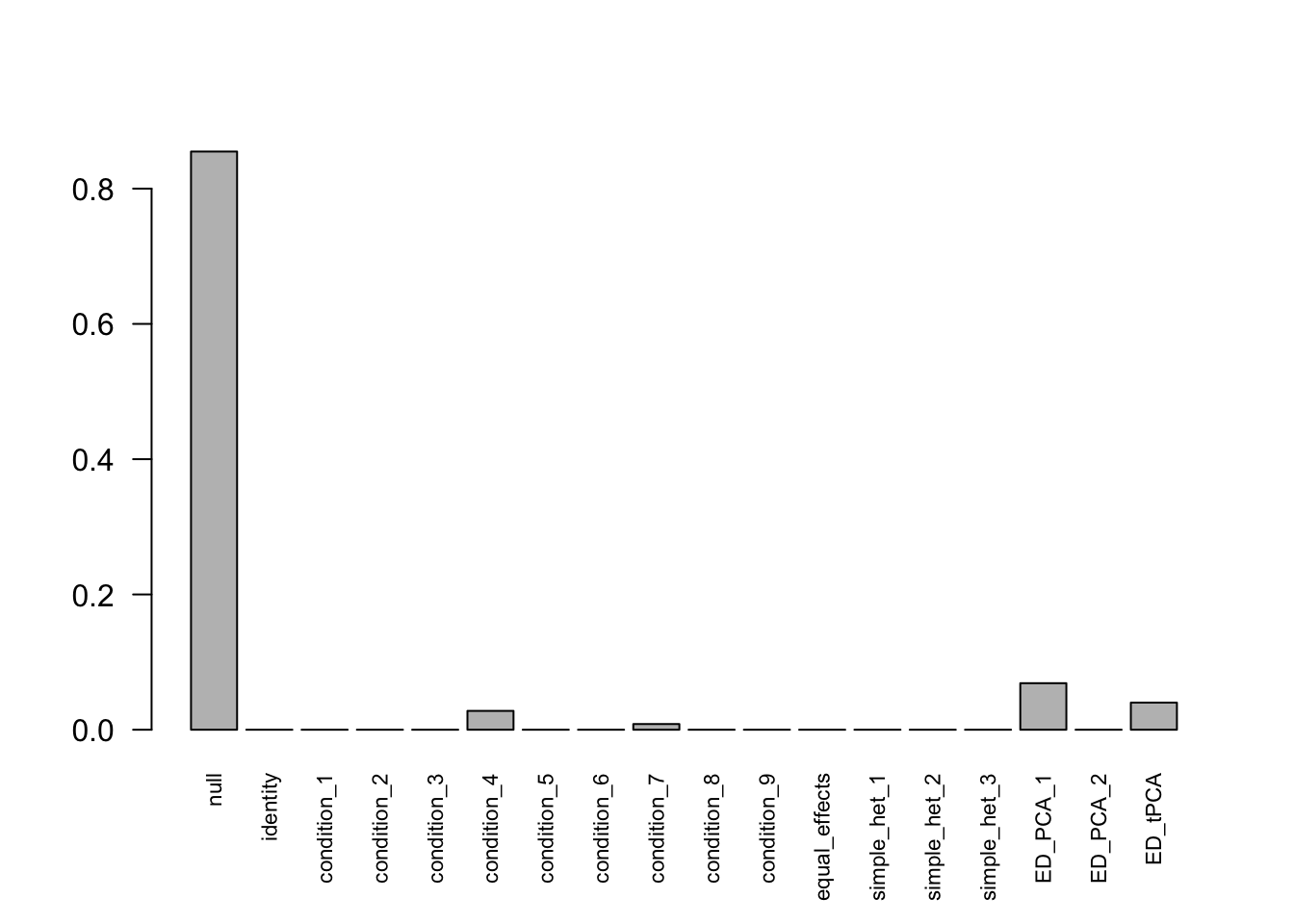

The correlation for PCA1 is: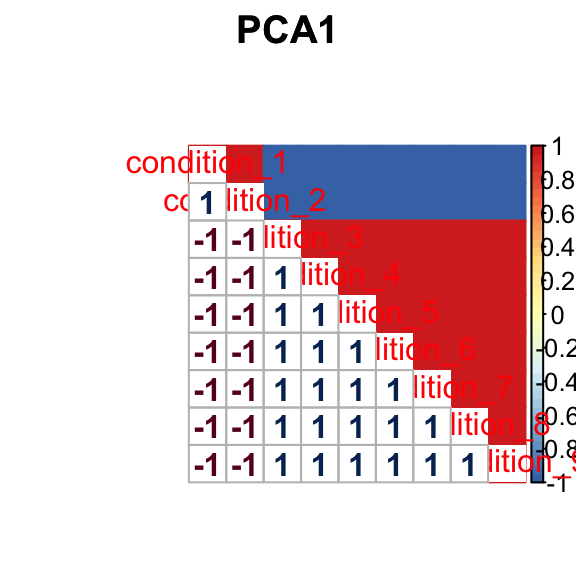

Recover the last column

mashcontrast.model.10.full = mashcontrast.model.10
mashcontrast.model.10.full$result = mash_compute_posterior_matrices(g = mashcontrast.model.10, data = mash_data_L.10, algorithm.version = 'R', recover=TRUE)

There are 289 discoveries.

  • Original estimates

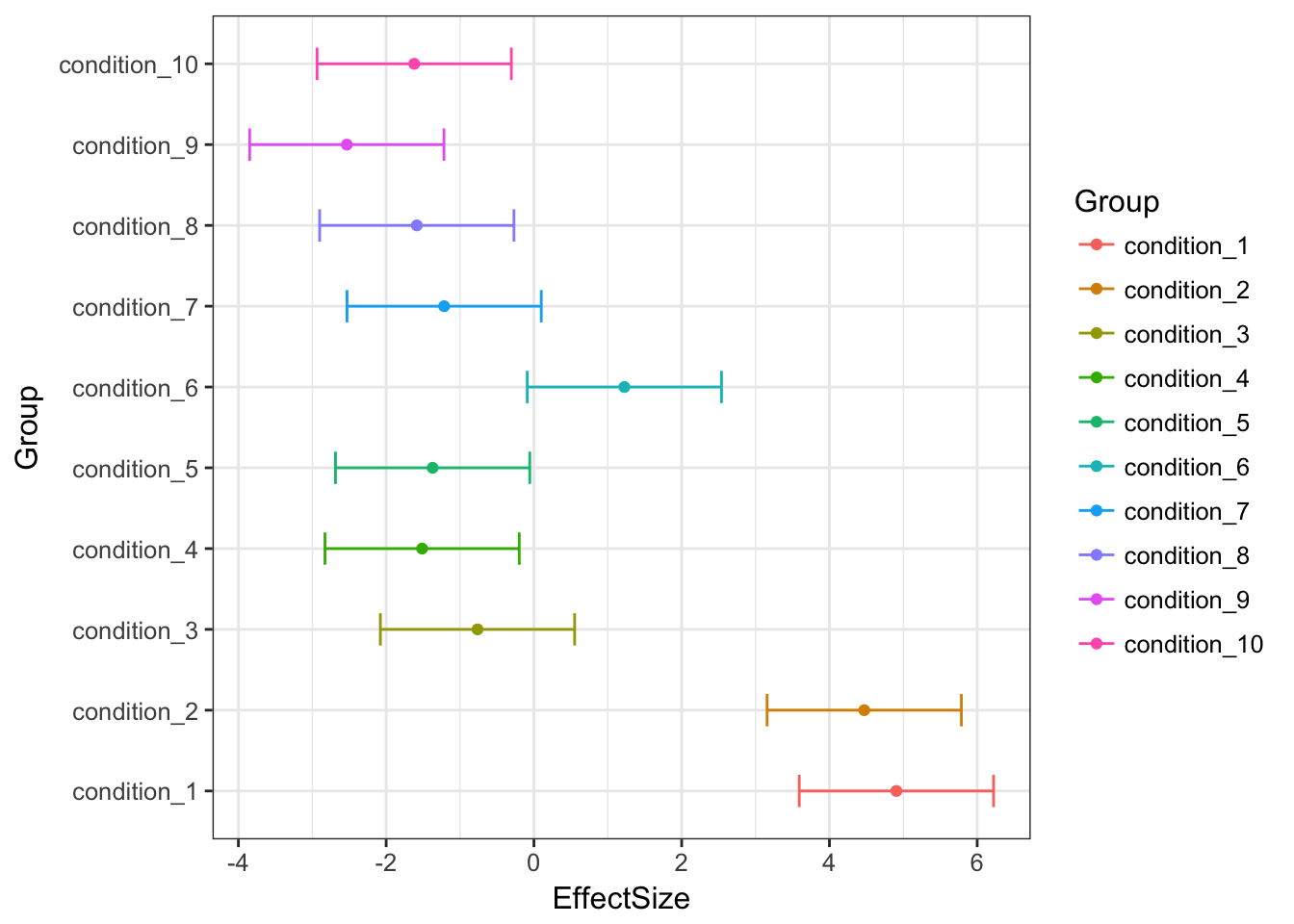
  • MASH estimates

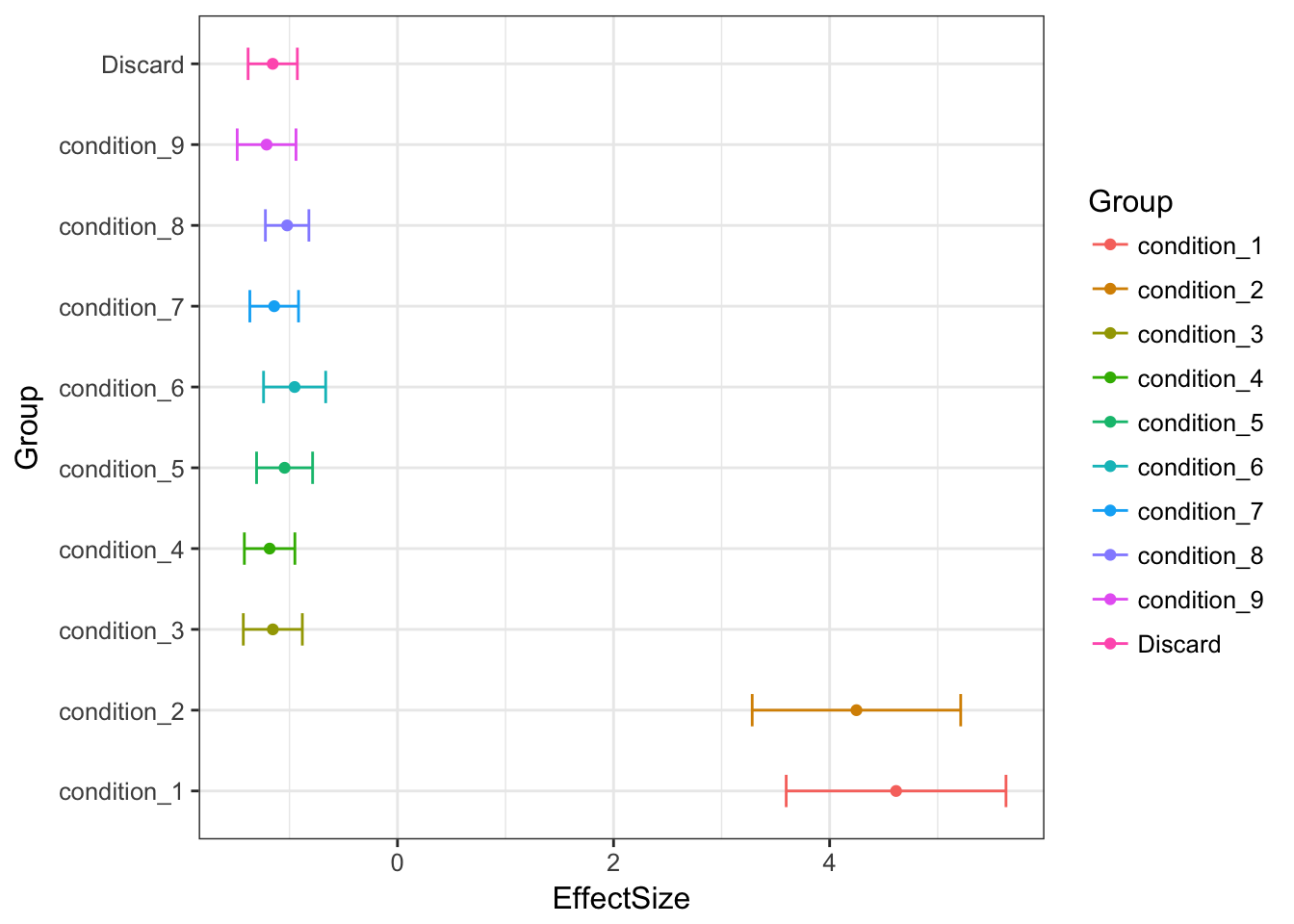
Subtract mean directly

If we subtract the mean from the data directly \[Var(\hat{c}_{j,r}-\bar{\hat{c}_{j}}) = \frac{1}{2} - \frac{1}{2R}\]

Indep.data.10 = mash_set_data(Bhat = mash_data_L.10$Bhat,
                           Shat = matrix(sqrt(0.5-1/(2*R)), nrow(data$Chat), R-1))

Indep.model.10 = mash(Indep.data.10, c(U.c, U.ed), algorithm.version = 'R', verbose = FALSE)

There are 336 discoveries. The covariance structure found here is:

barplot(get_estimated_pi(Indep.model.10),las = 2, cex.names = 0.7)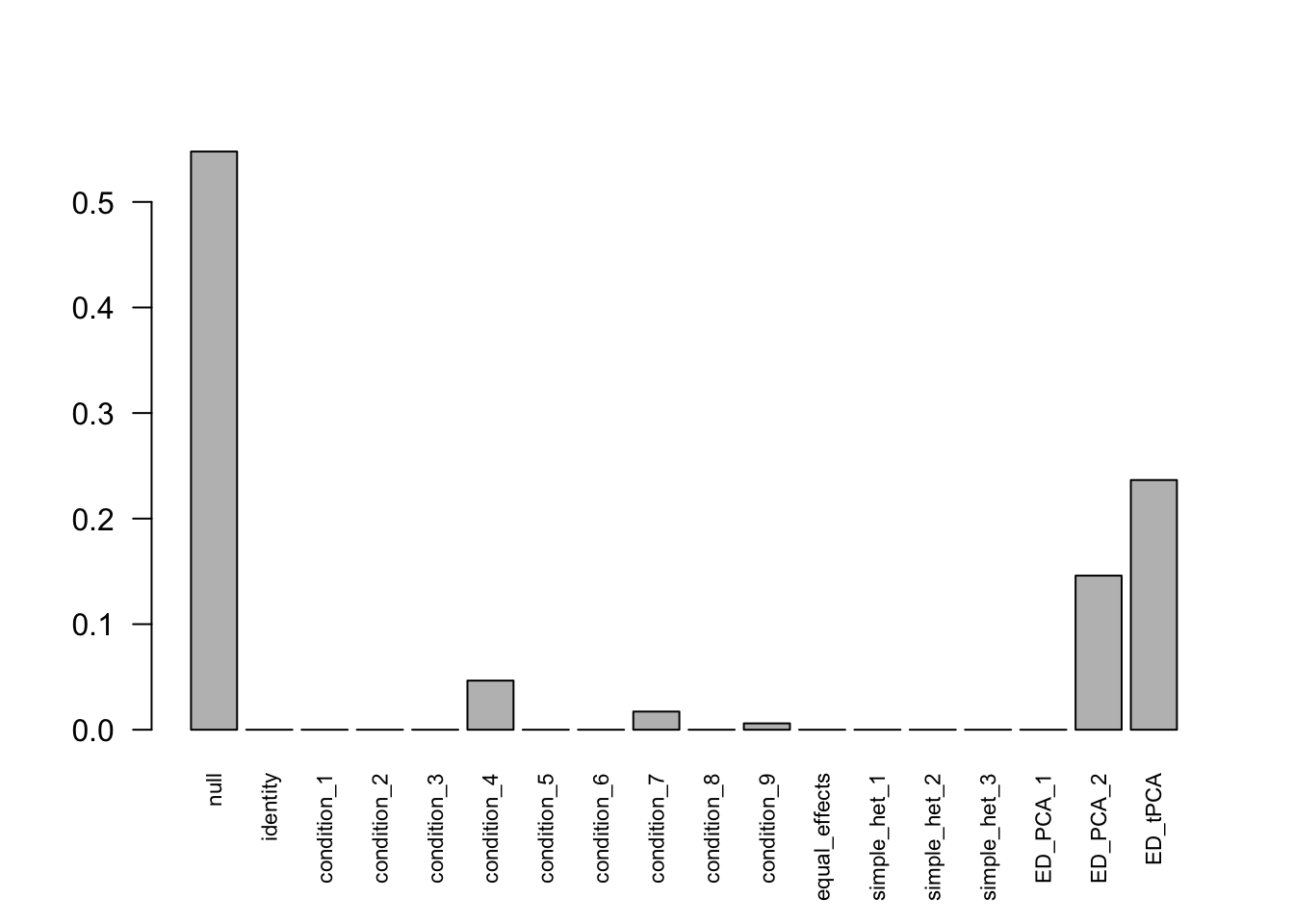

The correlation for PCA2 and tPCA is: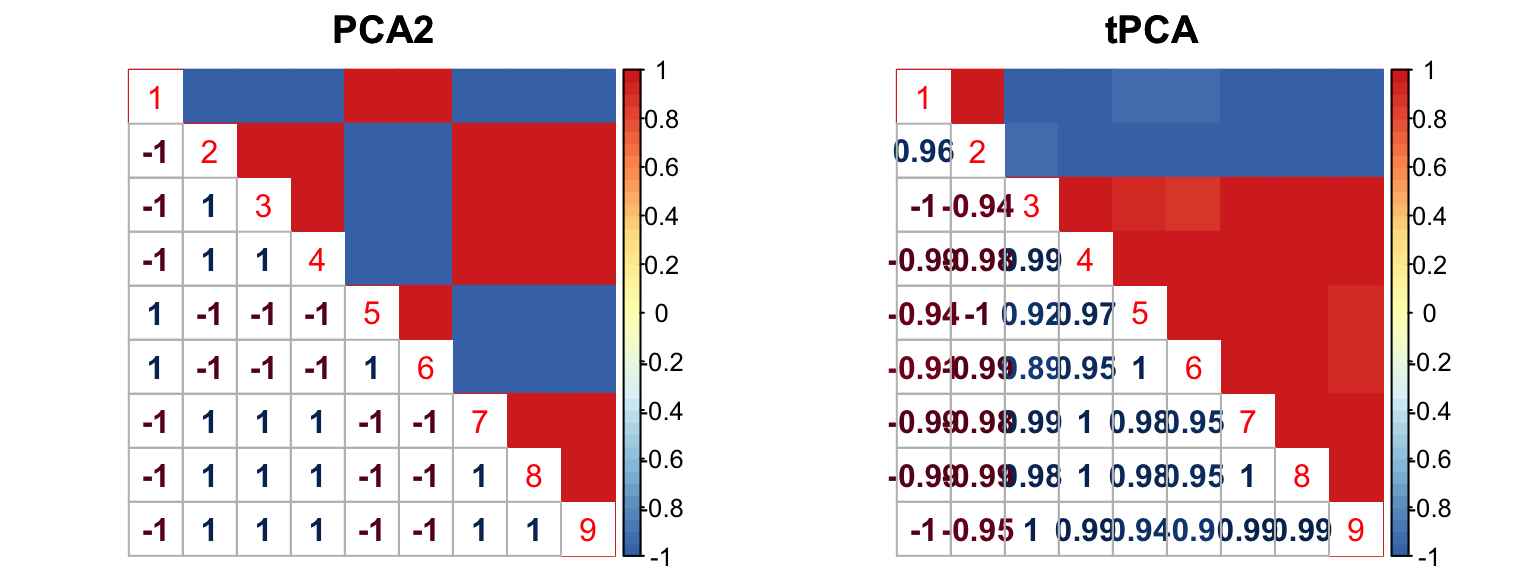

Recover the last column

Indep.model.10.full = Indep.model.10
Indep.model.10.full$result = mash_compute_posterior_matrices(g = Indep.model.10, data = Indep.data.10, algorithm.version = 'R', recover=TRUE)

There are 336 discoveries.

Miscalculation of variance of mean

We try an example with the miscalculated variance of mean. The reason to include this example is that the variance of median is hard to compute (not iid data), if we subtract median from the samples directly. We want to test whether the misspecified variance could influence the result.

The following model is fitted under miscalculation of \(Var(\hat{c}_{j,r}-\bar{\hat{c}_{j}}) = \frac{1}{2}\).

There are 283 discoveries. The covariance structure found here is: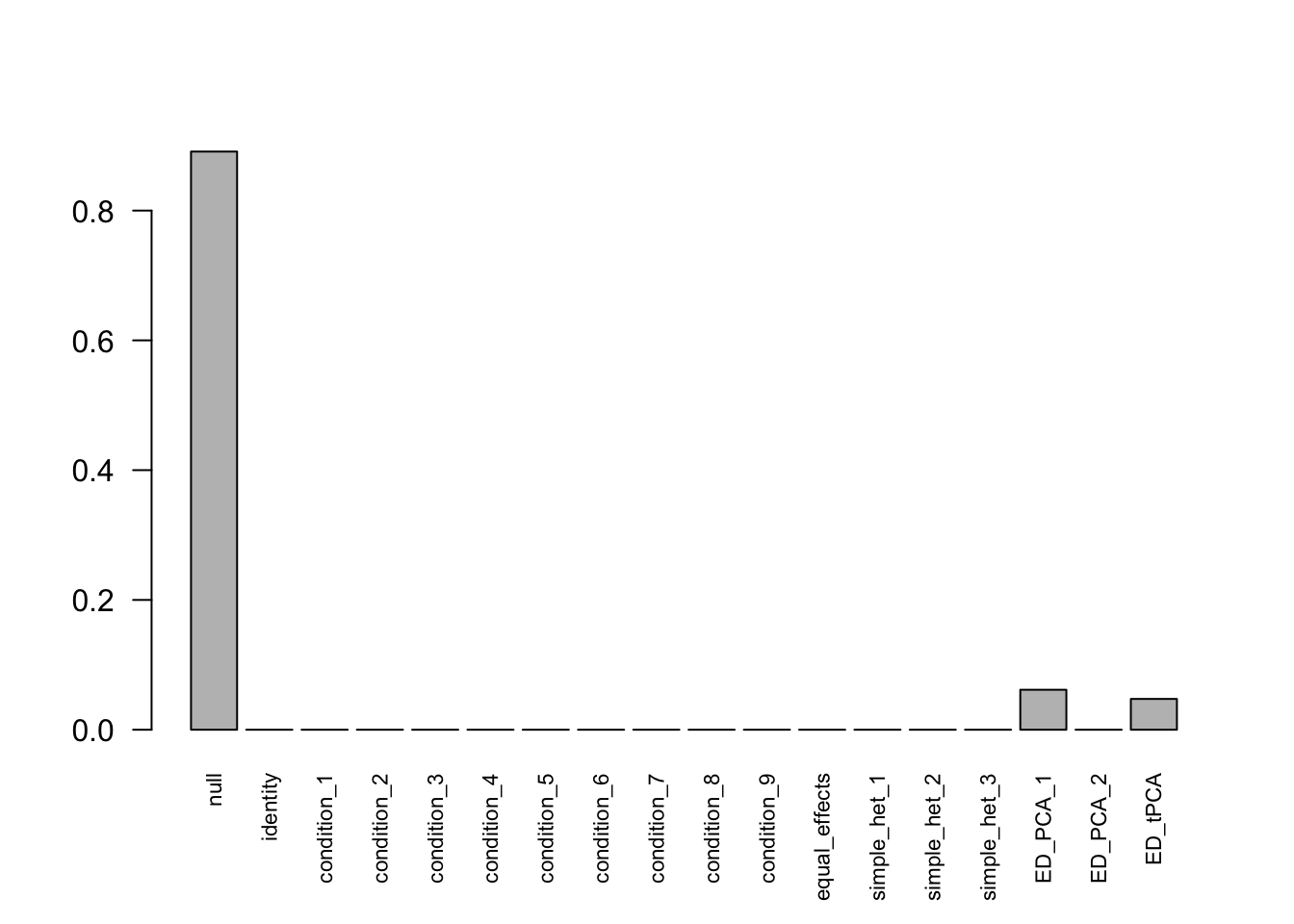

Recover the last column

Mis.model.10.full = Mis.model.10
Mis.model.10.full$result = mash_compute_posterior_matrices(g = Mis.model.10, data = Mis.data.10, algorithm.version = 'R', recover=TRUE)

There are 283 discoveries.

Discard the first column

The data was generated with signals in the first c conditions (\(c_{j,1}, \cdots, c_{j,c}\)). The contrast matrix L used here discards the last condition among R conditions. The deviations are \(\hat{c}_{j,1} - \bar{\hat{c}_{j}}, \hat{c}_{j,2} - \bar{\hat{c}_{j}}, \cdots, \hat{c}_{j,R-1} - \bar{\hat{c}_{j}}\).

However, the contrast matrix L can discard any deviation from \(\hat{c}_{j,1} - \bar{\hat{c}_{j}}, \cdots, \hat{c}_{j,R} - \bar{\hat{c}_{j}}\). The choice of the discarded deviation could influence the result.

We run the same model with L that discard the first deviation.

Mash contrast model

L.1 = L[2:R,]
mash_data_L.1 = mash_set_data_contrast(mash_data, L.1)
U.c = cov_canonical(mash_data_L.1)

# data driven
# select max
m.1by1.1 = mash_1by1(mash_data_L.1)
strong = get_significant_results(m.1by1.1,0.05)
# center Z
mash_data_L.center = mash_data_L.1
mash_data_L.center$Bhat = mash_data_L.1$Bhat/mash_data_L.1$Shat # obtain z
mash_data_L.center$Shat = matrix(1, nrow(mash_data_L.1$Bhat),ncol(mash_data_L.1$Bhat))
mash_data_L.center$Bhat = apply(mash_data_L.center$Bhat, 2, function(x) x - mean(x))
U.pca = cov_pca(mash_data_L.center,2,strong)
U.ed = cov_ed(mash_data_L.center, U.pca, strong)

mashcontrast.model.1 = mash(mash_data_L.1, c(U.c, U.ed), algorithm.version = 'R', verbose = FALSE)

Using mashcommonbaseline model, there are 283 discoveries. The covariance structure found here is:

barplot(get_estimated_pi(mashcontrast.model.1),las = 2, cex.names = 0.7)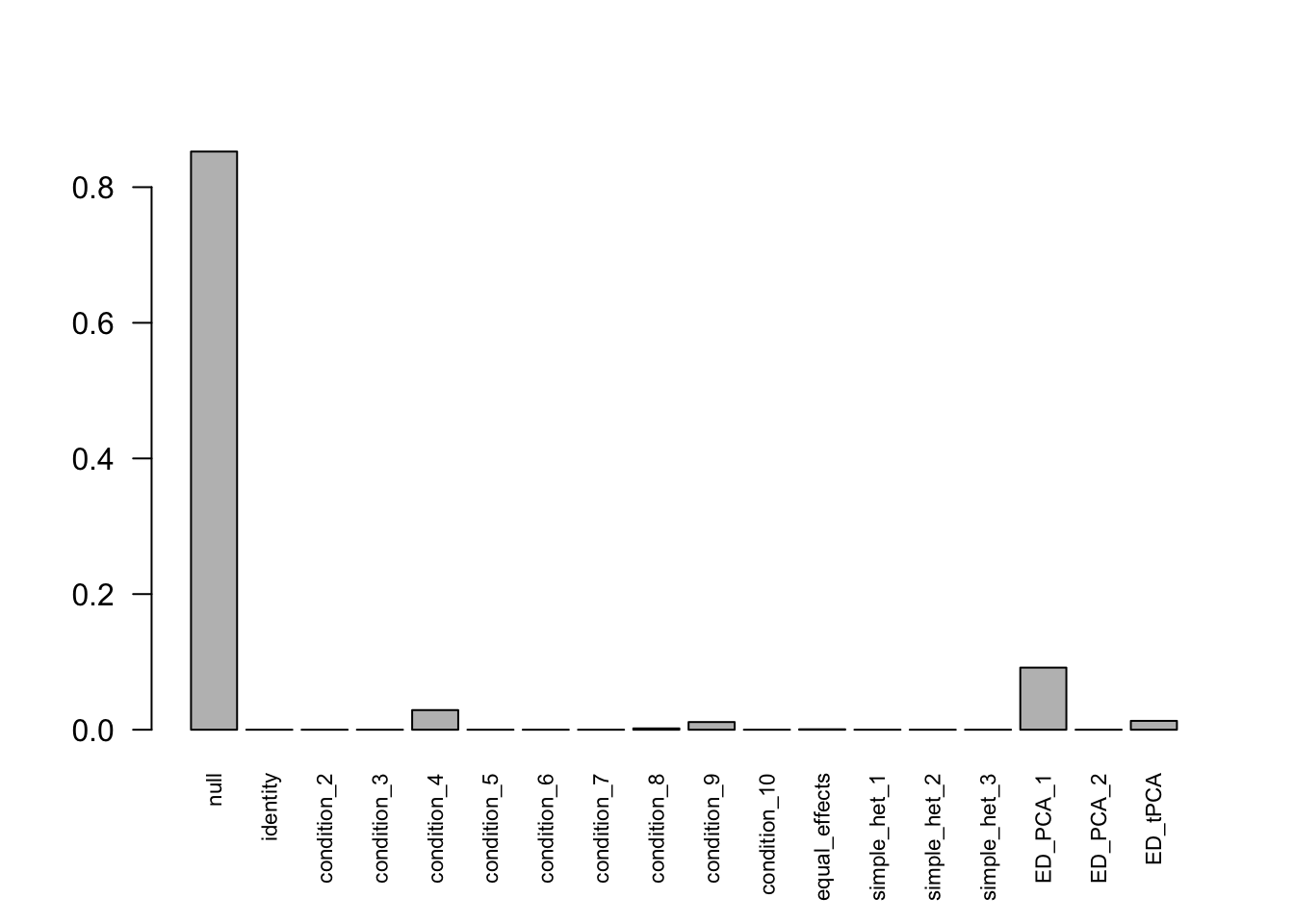

The correlation PCA 1 is: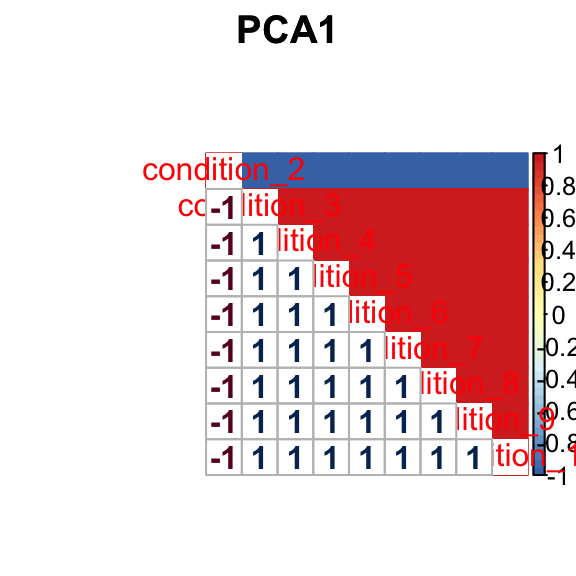

Recover the first column

mashcontrast.model.1.full = mashcontrast.model.1
mashcontrast.model.1.full$result = mash_compute_posterior_matrices(g = mashcontrast.model.1, data = mash_data_L.1, algorithm.version = 'R', recover=TRUE)

There are 285 discoveries.

Subtract mean directly

Indep.data.1 = mash_set_data(Bhat = mash_data_L.1$Bhat,
                           Shat = matrix(sqrt(0.5-1/(R*2)), nrow(data$Chat), R-1))

Indep.model.1 = mash(Indep.data.1, c(U.c, U.ed), algorithm.version = 'R', verbose = FALSE)

For mashIndep model, there are 217 discoveries. The covariance structure found here is:

barplot(get_estimated_pi(Indep.model.1),las = 2, cex.names = 0.7)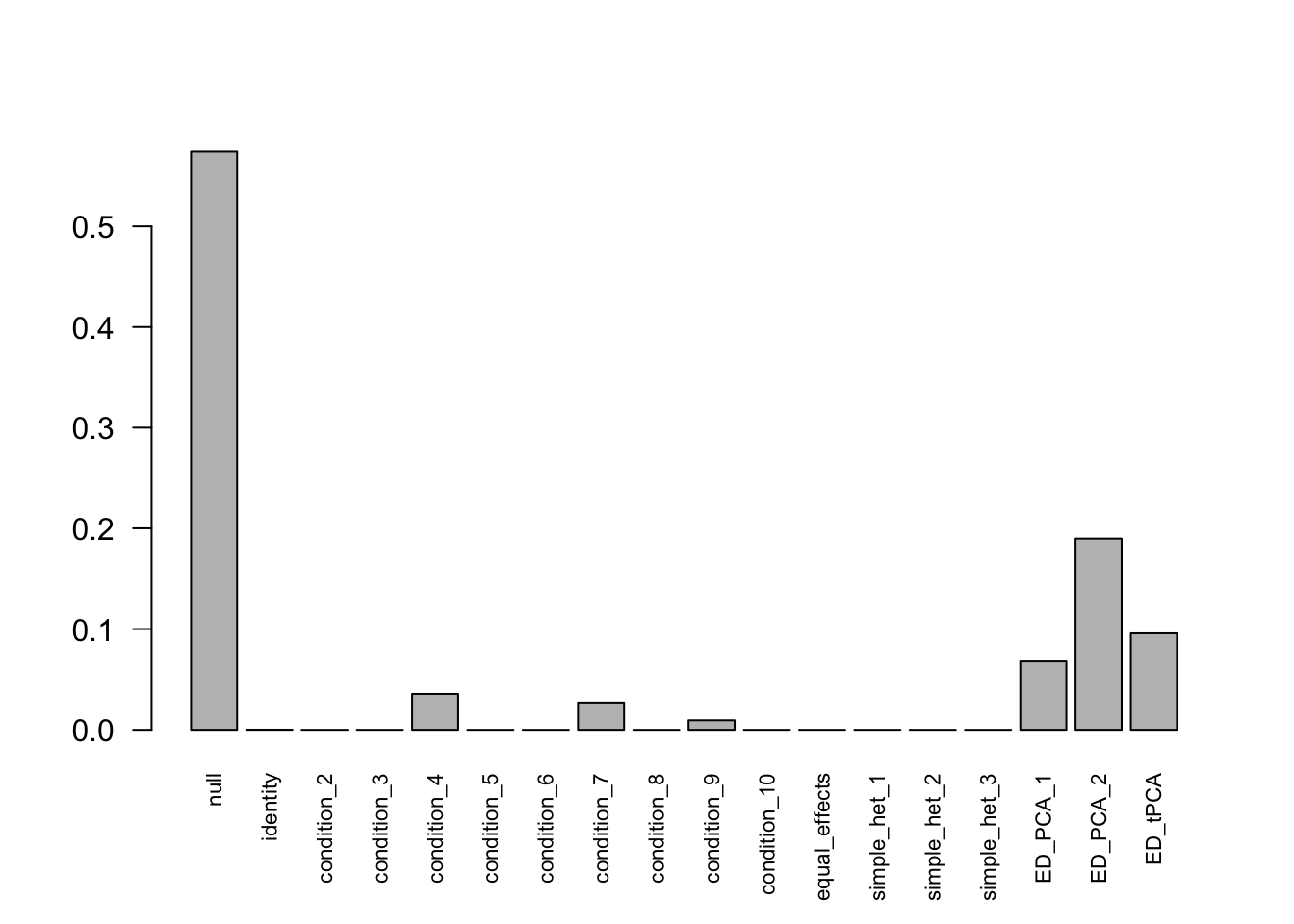

The correlation for PCA2 and tPCA is: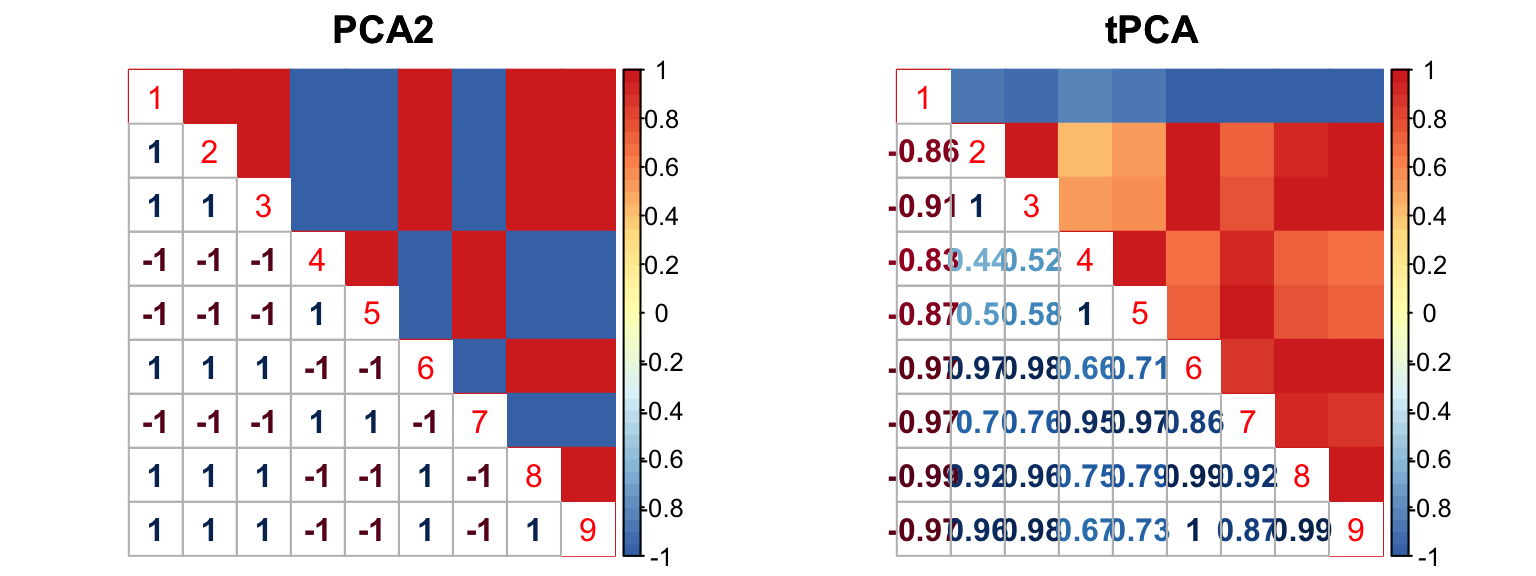

Recover the first column

Indep.model.1.full = Indep.model.1
Indep.model.1.full$result = mash_compute_posterior_matrices(g = Indep.model.1, data = Indep.data.1, algorithm.version = 'R', recover=TRUE)

There are 219 discoveries.

Miscalculation of variance of mean

The following model is fitted under miscalculation of \(Var(\hat{c}_{j,r}-\bar{\hat{c}_{j}}) = \frac{1}{2}\).

There are 168 discoveries. The covariance structure found here is: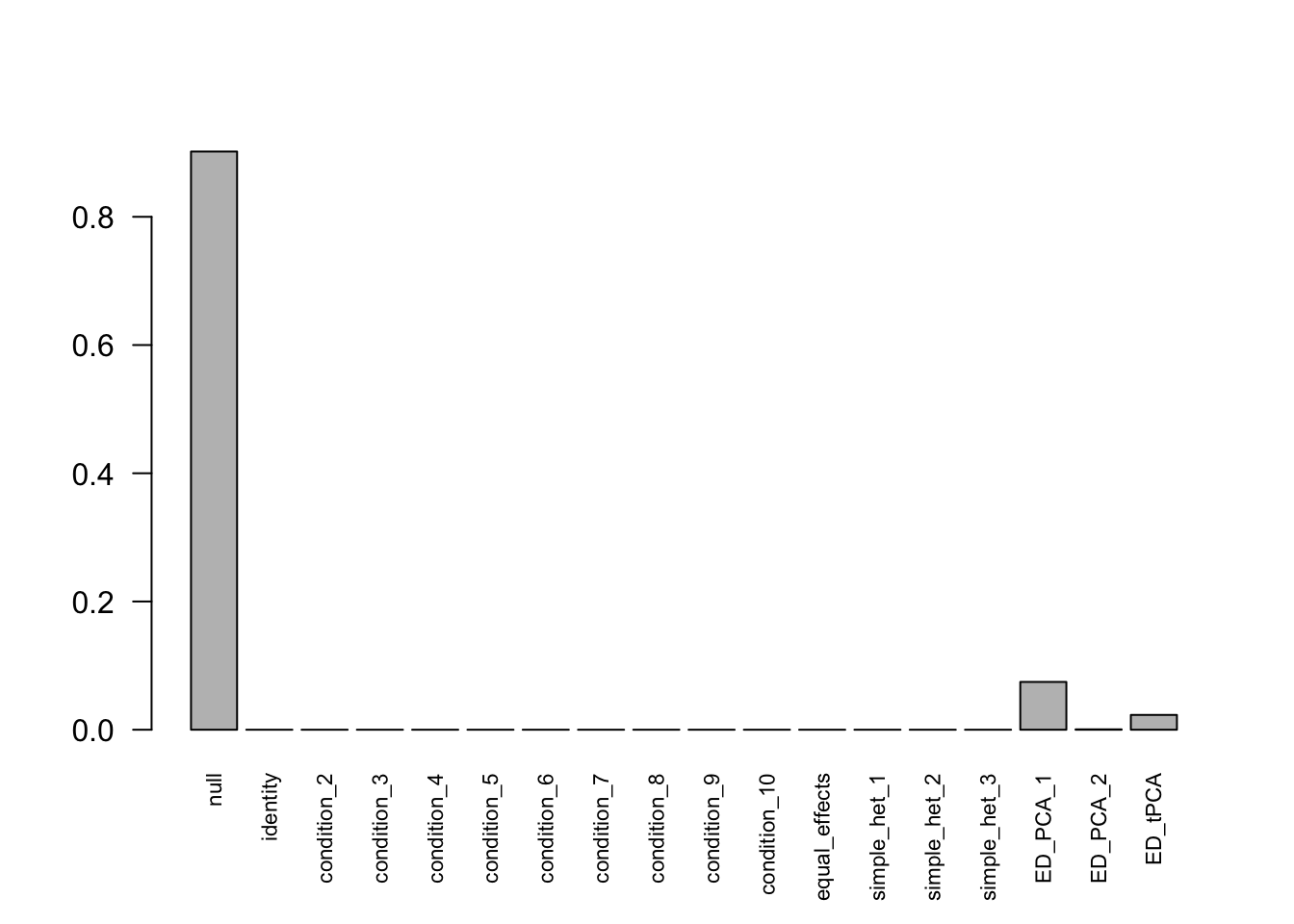

Recover the first column

Mis.model.1.full = Mis.model.1
Mis.model.1.full$result = mash_compute_posterior_matrices(g = Mis.model.1, data = Mis.data.1, algorithm.version = 'R', recover=TRUE)

There are 283 discoveries.

Compare models

The RRMSE plot:

delta.10 = data$C - rowMeans(data$C)
deltahat.10 = data$Chat - rowMeans(data$Chat)

delta.1 = delta.10[, c(2:10, 1)]
deltahat.1 = deltahat.10[, c(2:10, 1)]

barplot(c(sqrt(mean((delta.10 - m.1by1$result$PosteriorMean)^2)/mean((delta.10 - deltahat.10)^2)),
          sqrt(mean((delta.10 - mashcontrast.model.10.full$result$PosteriorMean)^2)/mean((delta.10 - deltahat.10)^2)), 
          sqrt(mean((delta.1 - mashcontrast.model.1.full$result$PosteriorMean)^2)/mean((delta.1 - deltahat.1)^2)), 
          sqrt(mean((delta.10 - Indep.model.10.full$result$PosteriorMean)^2)/mean((delta.10 - deltahat.10)^2)),
          sqrt(mean((delta.1 - Indep.model.1.full$result$PosteriorMean)^2)/mean((delta.1 - deltahat.1)^2)), 
          sqrt(mean((delta.10 - Mis.model.10.full$result$PosteriorMean)^2)/mean((delta.10 - deltahat.10)^2)), 
          sqrt(mean((delta.1 - Mis.model.1.full$result$PosteriorMean)^2)/mean((delta.1 - deltahat.1)^2))), ylim=c(0,0.3), names.arg = c('ash','common.10','common.1','mash.10', 'mash.1', 'mis.10', 'mis.1'), las=2, cex.names = 0.7)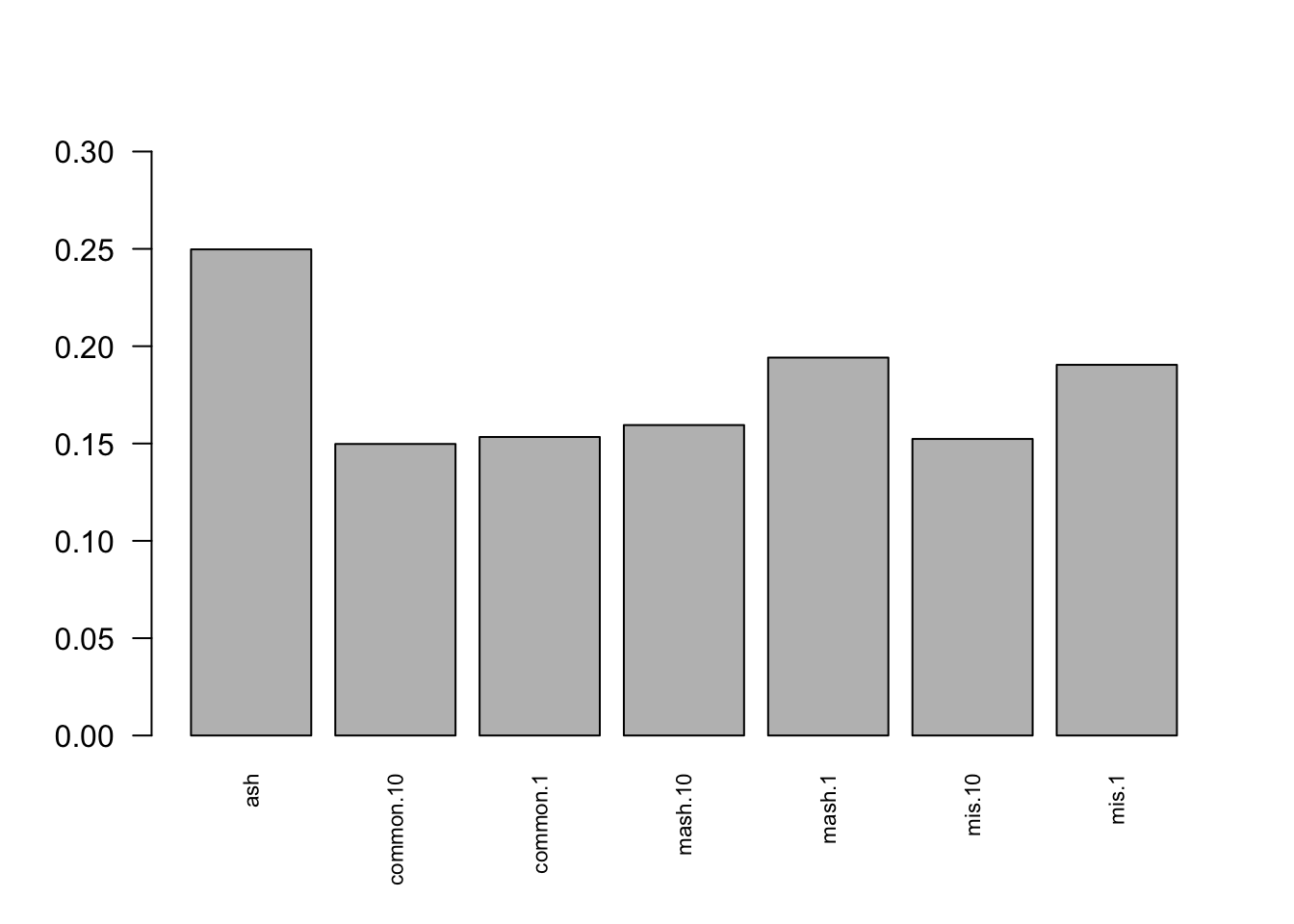

We check the False Positive Rate and True Positive Rate. \[FPR = \frac{|N\cap S|}{|N|} \quad TPR = \frac{|CS\cap S|}{|T|} \]

sign.test.ash = as.matrix(delta.10)*m.1by1$result$PosteriorMean
sign.test.mash.10 = as.matrix(delta.10)*mashcontrast.model.10.full$result$PosteriorMean
sign.test.Indep.10 = as.matrix(delta.10)*Indep.model.10.full$result$PosteriorMean
sign.test.Mis.10 = as.matrix(delta.10)*Mis.model.10.full$result$PosteriorMean
sign.test.mash.1 = as.matrix(delta.1)*mashcontrast.model.1.full$result$PosteriorMean
sign.test.Indep.1 = as.matrix(delta.1)*Indep.model.1.full$result$PosteriorMean
sign.test.Mis.1 = as.matrix(delta.1)*Mis.model.1.full$result$PosteriorMean


thresh.seq = seq(0, 1, by=0.0005)[-1]
Ash = matrix(0,length(thresh.seq), 2)
mashcontrast.1 = matrix(0,length(thresh.seq), 2)
Indep.1 = matrix(0,length(thresh.seq), 2)
Mis.1 = matrix(0,length(thresh.seq), 2)
mashcontrast.10 = matrix(0,length(thresh.seq), 2)
Indep.10 = matrix(0,length(thresh.seq), 2)
Mis.10 = matrix(0,length(thresh.seq), 2)
colnames(mashcontrast.1) = colnames(Mis.10) = colnames(Mis.1) = colnames(Ash) = c('TPR', 'FPR')
colnames(Indep.1) = c('TPR', 'FPR')
colnames(mashcontrast.10) = c('TPR', 'FPR')
colnames(Indep.10) = c('TPR', 'FPR')
for(t in 1:length(thresh.seq)){
  Ash[t,] = c(sum(sign.test.ash>0 & m.1by1$result$lfsr <= thresh.seq[t])/sum(delta.10!=0), sum(delta.10==0 & m.1by1$result$lfsr <=thresh.seq[t])/sum(delta.10==0))
  
  mashcontrast.1[t,] = c(sum(sign.test.mash.1>0 & mashcontrast.model.1.full$result$lfsr <= thresh.seq[t])/sum(delta.1!=0), sum(delta.1==0 & mashcontrast.model.1.full$result$lfsr <=thresh.seq[t])/sum(delta.1==0))
  
  Indep.1[t,] = c(sum(sign.test.Indep.1>0& Indep.model.1.full$result$lfsr <=thresh.seq[t])/sum(delta.1!=0),  sum(delta.1==0& Indep.model.1.full$result$lfsr <=thresh.seq[t])/sum(delta.1==0))
  
  Mis.1[t,] = c(sum(sign.test.Mis.1>0 & Mis.model.1.full$result$lfsr <= thresh.seq[t])/sum(delta.1!=0), sum(delta.1==0 & Mis.model.1.full$result$lfsr <=thresh.seq[t])/sum(delta.1==0))
  
  mashcontrast.10[t,] = c(sum(sign.test.mash.10>0 & mashcontrast.model.10.full$result$lfsr <= thresh.seq[t])/sum(delta.10!=0), sum(delta.10==0 & mashcontrast.model.10.full$result$lfsr <=thresh.seq[t])/sum(delta.10==0))
  
  Indep.10[t,] = c(sum(sign.test.Indep.10>0& Indep.model.10.full$result$lfsr <=thresh.seq[t])/sum(delta.10!=0),  sum(delta.10==0& Indep.model.10.full$result$lfsr <=thresh.seq[t])/sum(delta.10==0))
  
  Mis.10[t,] = c(sum(sign.test.Mis.10>0& Mis.model.10.full$result$lfsr <=thresh.seq[t])/sum(delta.10!=0),  sum(delta.10==0& Mis.model.10.full$result$lfsr <=thresh.seq[t])/sum(delta.10==0))
}

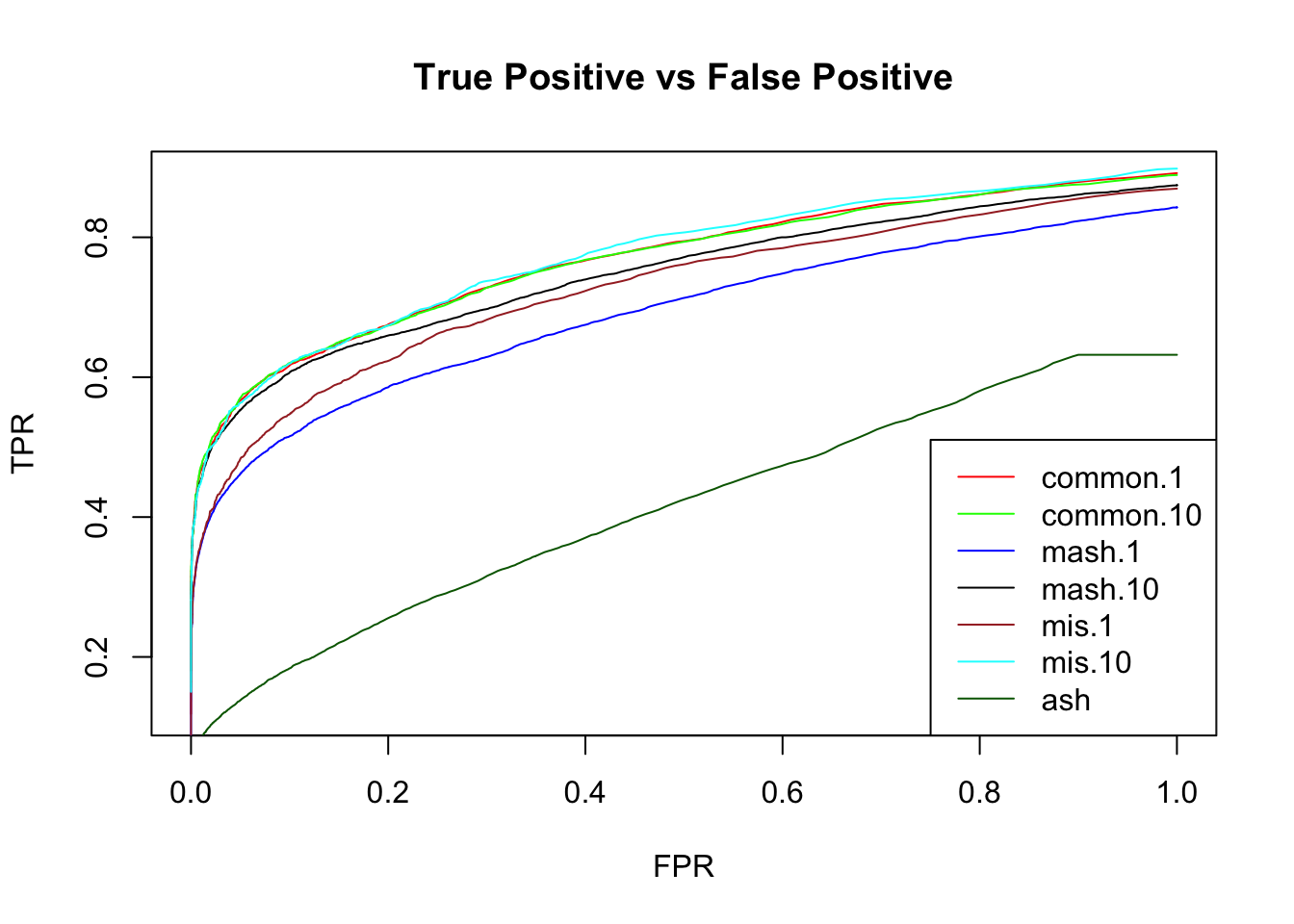
The mashcommonbaseline model performs better than mash.indep model. The choice of the discarded column has larger effect for mash.indep model.

Session information

sessionInfo()
R version 3.4.4 (2018-03-15)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.4

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] mvtnorm_1.0-7    plyr_1.8.4       assertthat_0.2.0 ggplot2_2.2.1   
[5] corrplot_0.84    mashr_0.2-8      ashr_2.2-7      

loaded via a namespace (and not attached):
 [1] Rcpp_0.12.16             pillar_1.2.2            
 [3] compiler_3.4.4           git2r_0.21.0            
 [5] iterators_1.0.9          tools_3.4.4             
 [7] digest_0.6.15            evaluate_0.10.1         
 [9] tibble_1.4.2             gtable_0.2.0            
[11] lattice_0.20-35          rlang_0.2.0             
[13] Matrix_1.2-14            foreach_1.4.4           
[15] yaml_2.1.19              parallel_3.4.4          
[17] stringr_1.3.0            knitr_1.20              
[19] REBayes_1.3              rprojroot_1.3-2         
[21] grid_3.4.4               rmarkdown_1.9           
[23] rmeta_3.0                magrittr_1.5            
[25] backports_1.1.2          scales_0.5.0            
[27] codetools_0.2-15         htmltools_0.3.6         
[29] MASS_7.3-50              colorspace_1.3-2        
[31] labeling_0.3             stringi_1.2.2           
[33] Rmosek_8.0.69            lazyeval_0.2.1          
[35] pscl_1.5.2               doParallel_1.0.11       
[37] munsell_0.4.3            truncnorm_1.0-8         
[39] SQUAREM_2017.10-1        ExtremeDeconvolution_1.3

This R Markdown site was created with workflowr